9 6 Jacks Or Better Video Poker Trainer

More Games Select from 19 different video poker variations with the button, including Jacks or Better, Bonus, Double Double, Triple Double, Full Pay Deuces, 16/10 (Not So Ugly) Deuces, Loose Deuces, three kinds of Joker Poker, and more. Keyboard You can use the mouse to click on cards to hold, or you may find it easier to use the keyboard. 9/6 Jacks or Better is the Jacks or Better game to play because that’s the game with the best payout percentage for the player. (It’s called a full pay machine.) The expected return on a 9/6 Jacks or Better game is 99.54%, which means for every $100 you wager, over time, your expected loss is only 46 cents.

9/6 Jacks or Better is the Jacks or Better game to play because that’s the game with the best payout percentage for the player. (It’s called a full pay machine.)

The expected return on a 9/6 Jacks or Better game is 99.54%, which means for every $100 you wager, over time, your expected loss is only 46 cents. Join a slots club and get an additional 0.1% or 0.2% back, and you’re looking at losing only a quarter or so on every $100 you wager. That’s some of the best odds in the casino.

Jacks Or Better Trainer

What is 9/6 Jacks or Better Though?

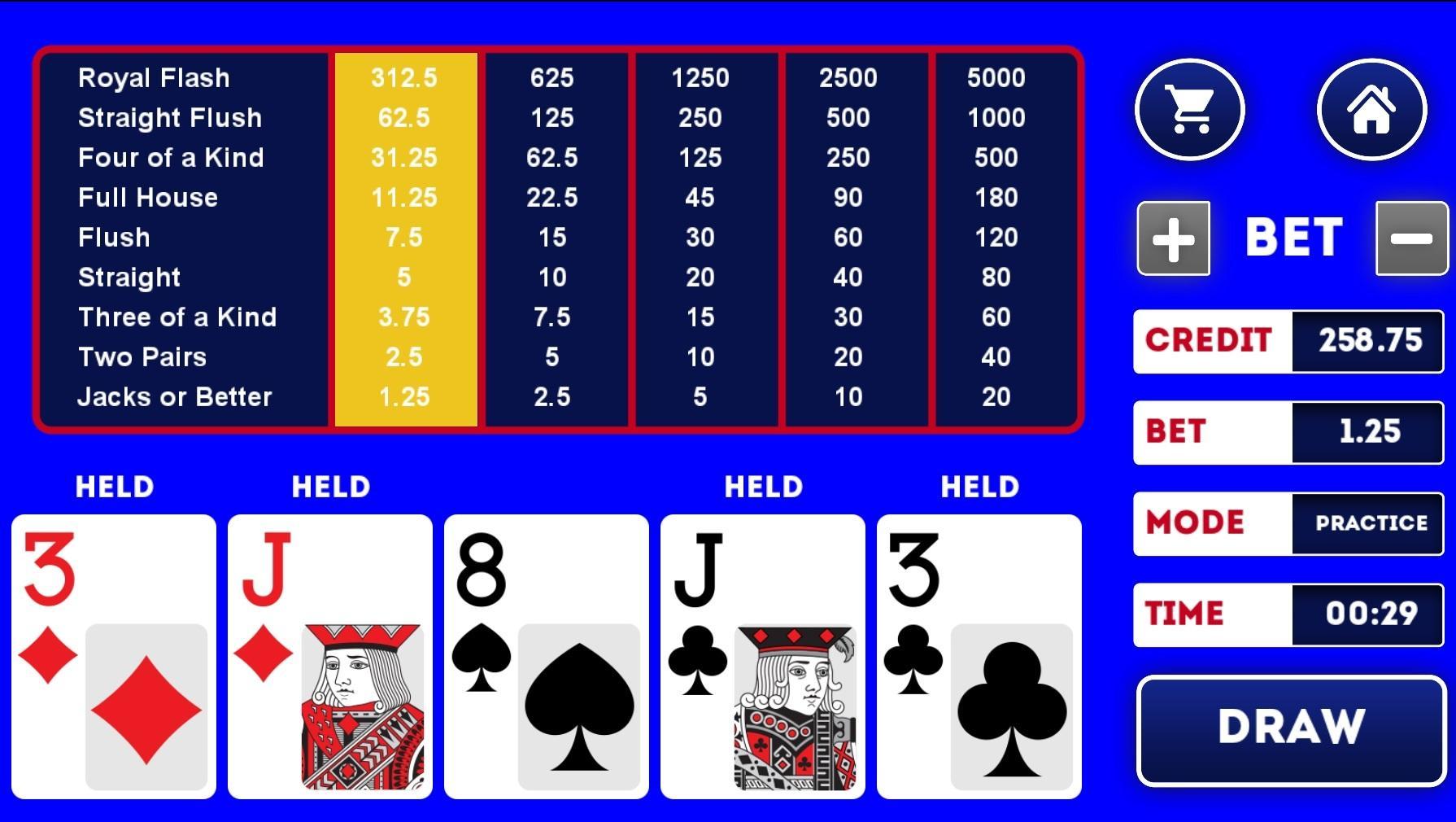
A “9/6 Jacks or Better” game pays out 9 coins for a 1 coin bet on a full house, and 6 coins for a 1 coin bet on a flush. This makes it easy to figure out, because you only have to look at the payout on 2 different hands. (When you’re looking at Deuces Wild, for example, the payouts can vary all over the place for all kinds of different hands.)

8/5 Jacks or Better

An 8/5 Jacks or Better game only pays out 8 coins for a 1 coin bet on a full house, and 5 coins for a 1 coin bet on a flush. This drops the expected return on the game from a healthy 99.54% to an anemic 97.30%. A 97.30% return sounds great until you look at the difference between that and a 99.54% return.

While you’re losing 46 cents for every $100 you bet with the 9/6 Jacks or Better game, you’re losing $2.70 for every $100 you bet on the 8/5 Jacks or Better game. That means you’re losing 5 times as much money on every bet, over time. You might as well play a single zero roulette table, if you can find one.

7/5 Jacks or Better

Even though “8/5 Jacks or Better” is surprisingly common, 7/5 Jacks or Better is also surprisingly common. The expected return on a 7/5 Jacks or Better game is 96.15%. That means you’re giving up another $1.15 per every $100 you bet beyond what you already gave up when you decided to play 8/5 Jacks or Better.

6/5 Jacks or Better

Yes, it gets even worse. Some casinos do offer 6/5 Jacks or Better video poker, which only pays out 6 coins for a full house and 5 coins for a flush. The payout percentage for a 6/5 Jacks or Better game is 95%, which means you’re giving the casino $5 for every $100 you bet on the machine. That’s 10 times the average losses compared to a full pay 9/6 Jacks or Better game.

5/4 Jacks or Better

Believe it or not, some casinos even offer 5/4 Jacks or Better. That means a payout of 5 coins on a full house and 4 coins on a flush. The expected return on a 5/4 Jacks or Better game is only 92.78%, which means you’ll lose on average $7.22 for every $100 you wager on this machine. No thanks. I’ll play blackjack instead. Even an American roulette table with double zeros offers a better payback percentage than this.

As I mentioned last time, there are some important differences between these two Jacks or Better games. What makes their differences important is that a 99.66% 8/5/35 Jacks or Better game (misnamedBob Dancer is one of the world's foremost video poker experts. He is a regular columnist for Casino Player, Strictly Slots, and the Las Vegas Review-Journa land has written an autobiography and a novel about gambling. He provides advice for tens of thousands of casino enthusiasts looking to play video poker. Bob's website is www.bobdancer.com 'Bonus Poker' by IGT) is a better game than 99.54% 9/6 Jacks.

In 9/6 Jacks, for instance, 'QJ8', 'KQ9' and 'KJ9' are preferred to AKQJ. These are all 3-card straight flushes with two high cards and two gaps. In 8/5 Jacks (whether the quads return 25 or 35), 'QJ8' is preferred to AKQJ, but 'KQ9' and 'KJ9' are not.

The easy part of this, discussed last week, is that the 3-card straight flushes decrease in value by about 20¢ (for the 5-coin dollar player) when flushes pay 5 instead of 6. Since the value of the flush doesn't affect the value of AKQJ, it's no wonder that strategy isn't identical between the games.

The harder question is why is 'QJ8' higher than AKQJ and 'KQ9' lower. Both combinations are 3-card straight flushes with two high cards and two gaps. Why should they have different values?

If the other two cards in the hand were lower than an 8, 'QJ8' and 'KQ9' would have identical values. But when the other two cards are such that the hand includes AKQJ, things change. This is an example of a 'straight penalty'.

When we look at 'QJ8' (and the other two cards are AK), there are four 9s in the deck and four Ts which can be used to get straights. When we look at 'KQ9' (and the other two cards are AJ), there are three Js and four Ts to create straights. The reason we have few cards to make a straight is because we were dealt a J and threw it away.

This straight penalty is worth 7.4¢. Whether this is a major or trivial amount depends on your perspective. To me, every 7.4¢ counts.

Let's look closer at 3-card straight flushes when we go from 9/6 to 8/5. All 2-gap straight flushes (such as 'KT9', 'A35', or '357') change in value by 20.35¢. One-gap straight flushes (such as 'QJ9' or '457') change in value by 19.89¢, and the no-gappers (such as 'JT9' or '345') change by 19.43¢. Does this strike you as strange? Only the value of the flush changed. Why would this affect these straight flush draws differently?

When we draw two cards to any combination in a 52-card deck, there are exactly 1,081 different 2-card combinations we could draw. Drawing to any three spades, for example, there will be exactly 45 out of 1,081 combinations that will give us five spades. These 45 5-spade combinations may include a royal flush, one or more straight flushes and the rest will be regular flushes.

On the combinations we are considering, a royal flush is not possible, so the number of straight flushes and regular flushes must add up to 45. To a 2-gap straight flush (such as '347'), there is exactly one combination that will complete a straight flush (namely '56' in this case), so that means 44 regular flushes are possible. To a 1-gap straight flush (such as 'JT8'), there are exactly two combinations that complete the straight flush (namely 'Q9' and '97' in this case), so that means 43 regular flushes are possible. Starting with a no-gap straight flush (such as '678') there are three combinations to complete the straight flush (namely '45', '59' and '9T'), which means there will be 42 regular flushes.

Video Poker Jacks Are Better

One extra flush opportunity out of 1,081 chances on a dollar game amounts to 0.46¢ when we change the value of a flush by one unit. This is not a number worth memorizing, but understanding why different 3-card straight flush combinations are affected differently by a change in the value of a flush helps you memorize strategies. The more you understand about video poker, the more strategies 'make sense' rather than are just a jumble of unrelated rules.